10 Ein »einfacher« Faktorisierungsalgorithmus

Ich möchte hier nur kurz skizzieren, wie sich lineare Rekursionen prinzipiell anwenden lassen, um natürliche Zahlen zu faktorisieren.¹⁰

Wenn eine zusammengesetzte Zahl N = p ^. Q (mit p Primzahl und Q möglicherweise noch weiter zerlegbar) gegeben ist und K : = p - 1 (für (${\frac{{5}}{{p}}}$) = 1) bzw. K : = p + 1 (für (${\frac{{5}}{{p}}}$) = - 1) in viele kleine Teiler zerfällt¹¹, so haben wir eine Chance, den Primfaktor p über die Fibonaccifolge zu ermitteln: Wir konstruieren eine hochgradig in kleine Primzahlen¹² zerlegbare »riesengroße« Zahl h und hoffen darauf, daß diese durch K teilbar ist. Wenn wir Erfolg haben, ist dies der Fall. Dann aber gilt F_h $\equiv$ F_K $\equiv$ 0 ( mod p) und damit auch gcd(F_h, p) = p und wegen gcd(p, N) = p ist gcd(F_h, N) $\geq$ p. Mit einiger Wahrscheinlichkeit haben wir dann auch gcd(F_h, N) = p gefunden. Der Leser möge sich davon überzeugen, daß es ausreicht, F_h mod N zu berechnen; dies vermeidet eine explosionsartige Vergrößerung der Folgenwerte.

Der Algorithmus 2 bewerkstelligt das oben ausgeführte. Die »riesengroße« Zahl h wird dabei als Produkt kleinerer Zahlen h_i sukzessive aufgebaut; dies ermöglicht es, F_$\prod$hi mod N bereits in den Schleifendurchläufen zu ermitteln und die Schleife abzubrechen, wenn ein Faktor gefunden wird. Sobald ein Teiler von N gefunden ist, liefert fibfactor diesen als Ergebnis zurück; der gefundene Faktor ist nicht notwendigerweise eine Primzahl, in seltenen Fällen kann er sogar N selbst sein (z.B. für N : = F_q mit q prim und F_q zusammengesetzt (vgl. 5.4.1)). Auch ist nicht jeder gefundene Primfaktor notwendigerweise ±1 in kleine Teiler zerlegbar.¹³

10.0.1 Beispiel

Wählen wir p : = 12347 = 2^{2 .} 3^{2 .} 7³ - 1 und Q : = 100000127 = 2^{7 .} 3 ^. 260417 - 1; beides sind Primzahlen. Wir setzen N : = p ^. Q = 1234701568069. Nun »vergessen« wir die gewählten Faktoren und setzen den Algorithmus auf diese Zahl an. Wir wählen h : = 2^{3 .} 3^{3 .} 5^{3 .} 7³ = 9261000. Nun berechnen wir F_h mod N = 194310245762. Wir berechnen den größten gemeinsamen Teiler dieser Zahl mit N; es ergibt sich gcd(194310245762, N) = 12347. Nun prüfen wir (z.B. durch Probedivision), daß es sich bei p = 12347 um eine Primzahl handelt und stellen ferner fest: p + 1 = 2^{2 .} 3^{2 .} 7³. Wir dividieren den gefundenen Teiler ab und erhalten Q = ${\frac{{N}}{{p}}}$ = 100000127.

10.0.2 Bemerkungen:

Der angegebene Algorithmus cap:Faktorisierung-mit-Fibonaccizahlen kann als Template aufgefaßt werden, um strukturverwandte Faktorisierungsalgorithmen zu implementieren.

• Wenn man statt FIBPAIR den Datentyp NAT wählt und statt dem Startpaar fib=(1,0)= (F₁, F₀) eine Basis a wählt, so ergibt dies den klassischen p - 1-Algorithmus. (Es ist dann allerdings gcd(a - 1, N) anstelle von gcd(fib1, N) zu bilden.)
• Wenn man sich eine andere geeignete Multiplikation für FIBPAIR definiert, so erhält man andere Varianten des (p±1)-Algorithmus: Wählen Sie einfach eine andere lineare Rekursion der Form f_n : = c₁ ^. f_n-1 + c₂ ^. f_n-2. Wenn wir das charakteristische Polynom p_ch(x) : = x² - c₁ ^. x - c₂ betrachten und die Nullstellen berechnen, so erhalten wir x = ${\frac{{c_{1}\pm\sqrt{c_{1}^{2}+4c_{2}}}}{{2}}}$. 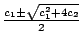Eine »Multiplikation« läßt sich dann durch x² = c₁x + c₂ konstruieren (vgl. Abschnitt 8). Für r : = c₁² +4c₂ können wir dann die Fälle (${\frac{{r}}{{p}}}$) = 1 bzw. (${\frac{{r}}{{p}}}$) = - 1 untersuchen. Dies wäre eine eher »experimentelle« Herleitung des (p + 1)-Algorithmus...
• Prinzipiell könnte man auch Folgen der Form f_n : = $\sum_{{i=1}}^{{k}}$c_i ^. f_n-i verwenden. Auch diese sind periodisch bezüglich Restklassenrechnung.¹⁴
• Wenn Sie statt FIBPAIR eine Datenstruktur für elliptische Kurven verwenden, so erhalten Sie ein Grundgerüst für den Faktorisierungsalgorithmus mit elliptischen Kurven, welches nur noch unwesentlicher Modifikation bedarf.¹⁵

10.0.3 Zusätzliche Hinweise und Ausblicke

In einer effizienten Implementierung wäre der oben angegebene Algorithmus nur die erste Phase eines komplexeren Algorithmus.

Man würde die Phase 1 nach einiger Zeit abbrechen, um nach einem einzelnen verbliebenen Restfaktor in der Zerlegung von K zu suchen. Der simple Ansatz führt auf die sogenannte »standard continuation«, dieser läßt sich zur »improved standard continuation« verbessern. Letzterer wiederum läßt sich mittels »Pairing« von zwei Zahlen in seiner Geschwindigkeit verdoppeln. Bei Fibonaccizahlen kann man hierzu Formel 9.3 benutzen. Eine weitere Effizienzsteigerung läßt sich erreichen, in dem man die einzelnen Faktoren (oder Faktorpaare) zusammenmultipliziert, bevor man den größten gemeinsamen Teiler berechnet. Dann lassen sich diese aber bei geeigneter Strukturierung als Nullstellen eines Polynoms (sehr hohen Grades) betrachten. Solche Polynome wiederum können unter Zuhilfenahme der diskreten Variante der schnellen Fouriertransformation ausgewertet werden (fft-continuation).

Alle diese Stufen habe ich für die (p-1)-Methode, für elliptische Kurven und nun auch für die Fibonacci-Methode implementiert. Sie sind Bestandteil eines Faktorisierungsprogramms, das ich auf meiner Homepage zum Download bereitgestellt habe.