- ... Reinecke1
- e-mail: reinecke@thorstenreinecke.de
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fibonacci-Folge2
- Sie sollten sich den Stammbaum aufzeichnen und die Rekursionsformel
über eine nach Geschlechtern getrennte Betrachtung herleiten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...3
- Der erste Mensch, der diese Eigenschaft »entdeckt« hat, wird natürlich
Ln : = Fn+1 + Fn-1 gesetzt und anschließend die zugehörigen
Startwerte ermittelt haben.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...4
- Es sei ausdrücklich erwähnt, daß die Induktion auf k basiert und damit
auch für negative Werte von n gültig ist!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gilt5
- Das ist übrigens eine sehr interessante Eigenschaft, wenn man FN
für zusammengesetzte N faktorisieren möchte!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... erhalten6
- Wir lassen hierfür auch reelle Zahlen als Folgenwerte zu und treffen
zusätzlich folgende Feststellungen:
Für alle Fibonaccifolgen f und g sowie jedem reellen Skalar
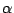 gilt:
gilt:
(
f 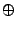 g
g)
n : =
fn +
gn =
fn-1 +
fn-2 +
gn-1 +
gn-2 = (
f 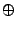 g
g)
n-1 + (
f 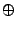 g
g)
n-2
(
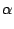
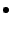 f
f )
n : =
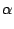 . fn
. fn =
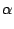 .
. (
fn-1 +
fn-2) =
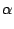 . fn-1
. fn-1 +
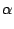 . fn-2
. fn-2 = (
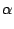
 f
f )
n-1 + (
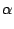
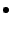 f
f )
n-2
Jede Linearkombination zweier gegebener Fibonaccifolgen ist somit
ebenfalls eine Fibonaccifolge. Die beiden Funktionsterme
(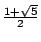 )n
sowie
(
)n
sowie
(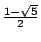 )n sind geschlossene Ausdrücke für
zwei verschiedene Fibonaccifolgen. Die nachfolgend aufgestellte Linearkombination
ist also die geschlossene Form einer Fibonaccifolge.
)n sind geschlossene Ausdrücke für
zwei verschiedene Fibonaccifolgen. Die nachfolgend aufgestellte Linearkombination
ist also die geschlossene Form einer Fibonaccifolge.
Etwas abstrakter betrachtet bilden die Fibonaccifolgen somit einen
zweidimensionalen Unterraum des (unendlichdimensionalen) Vektorraums
aller Folgen. Die beiden ausgewählten Funktionsterme bilden zusammen
ein Erzeugendensystem dieses zweidimensionalen Vektorraums.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...7
- Und tatsächlich wird ein derartiges Verfahren auch vom Matheprogramm
MAPLE verwendet, um Fibonaccifolgenwerte zu bestimmen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aufgerufen8
- Wenn in Restklassen gerechnet wird, dürfen sich diese nicht ändern.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Satzes9
-
(a + b)n =
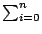
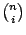 ai . bn-i mit Binomialkoeffizient
ai . bn-i mit Binomialkoeffizient
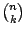 : =
: = 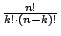 , bekannt aus dem Pascalschen
Dreieck
, bekannt aus dem Pascalschen
Dreieck
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...10
- Der explizite Ansatz, Fibonaccifolgen zu verwenden, ist eine Eigenkonstruktion
und in gewisser Weise eine Spezialisierung des in der Literatur bereits
hinlänglich bekannten (p+1)-Algorithmus.
Hier geht es weniger um ausgefeilte Effizienz als um die Grundidee!
Der interessierte Leser möge für Optimierungsansätze z.B. [PLMo87]
zu Rate ziehen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zerfällt11
- oder (ganz allgemein)
FK
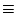 0 ( mod p) erfüllt ist (denn
wegen
F2n = FnLn können sich auch Teiler der Ln dazugesellen,
die nicht die obige Struktur aufweisen)
0 ( mod p) erfüllt ist (denn
wegen
F2n = FnLn können sich auch Teiler der Ln dazugesellen,
die nicht die obige Struktur aufweisen)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Primzahlen12
- Da kleine Primzahlen die gesuchte Zahl K möglicherweise mehrfach
teilen, mag es nicht nur erlaubt, sondern sogar erwünscht sein, wenn
sie auch in h mehrfach auftreten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...13
- Denn der Primfaktor kann auch Teiler einer in FK enthaltenen
Lucaszahl sein! Beispiel:
p : = 1974737795746080149567; es ist
p + 1 = 26 . 33 . 7 . 47 . 515894844583 . 6733,
aber es gilt trotzdem
gcd(F26 . 32 . 7, p) = p, weil
gcd(L25 . 32 . 7, p) = p ist...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...14
- Die Ermittlung der Multiplikationsformel und die Untersuchung der
Struktureigenschaften des charakteristischen Polynoms sollten Sie
dann allerdings einem Computeralgebrasystem überlassen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...15
- Dies dürfte auch der Grund dafür gewesen sein, warum Lenstra den genialen
Einfall hatte, elliptische Kurven zu verwenden: Er hat die Template-Eigenschaft
des (p-1)-Algorithmus erkannt und ihre Verwendbarkeit für elliptische
Kurven gesehen!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() gilt:
gilt:
![]() )n
sowie
(
)n
sowie
(![]() )n sind geschlossene Ausdrücke für
zwei verschiedene Fibonaccifolgen. Die nachfolgend aufgestellte Linearkombination
ist also die geschlossene Form einer Fibonaccifolge.
)n sind geschlossene Ausdrücke für
zwei verschiedene Fibonaccifolgen. Die nachfolgend aufgestellte Linearkombination
ist also die geschlossene Form einer Fibonaccifolge.